Tích phân không chỉ là một khái niệm trừu tượng trong toán học mà còn là một công cụ mạnh mẽ trong ngành công nghiệp. Trong nhiều lĩnh vực như xử lý tín hiệu, điều khiển quy trình, và thiết kế hệ thống, tích phân có vai trò rất lớn trong việc phân tích và hiểu rõ các hiện tượng xảy ra trong hệ thống.
Việc áp dụng tích phân trong kiểm soát quy trình là vô cùng quan trọng. Chẳng hạn, khi lập kế hoạch cho một hệ thống điều khiển nhiệt độ, các kỹ sư cần tính toán lượng năng lượng cần thiết để làm nóng hoặc làm lạnh một môi trường nhất định. Nếu không có kiến thức về tích phân, họ sẽ rất khó khăn trong việc xác định chính xác thông số nhiệt độ và thời gian cần thiết.
Ngoài ra, tích phân còn được sử dụng rộng rãi trong việc đánh giá hiệu suất của các hệ thống truyền động. Những phép đo tích phân giúp nhà kỹ thuật dự đoán cách các biến số ảnh hưởng đến nhau và từ đó đưa ra các phương án tối ưu cho thiết kế hệ thống.
Các Dạng Bài Tập Tích Phân Thường Gặp
Trong kỳ thi CPII, các dạng bài tập tích phân rất đa dạng và phong phú. Có thể chia thành các nhóm chính như sau:
- Tích phân bất định: Đây là dạng bài tập yêu cầu tìm nguyên hàm của một hàm số. Ví dụ, việc tìm nguyên hàm của hàm số f(x) = 3x^2 + 2x + 1 thường gặp trong các câu hỏi trắc nghiệm.
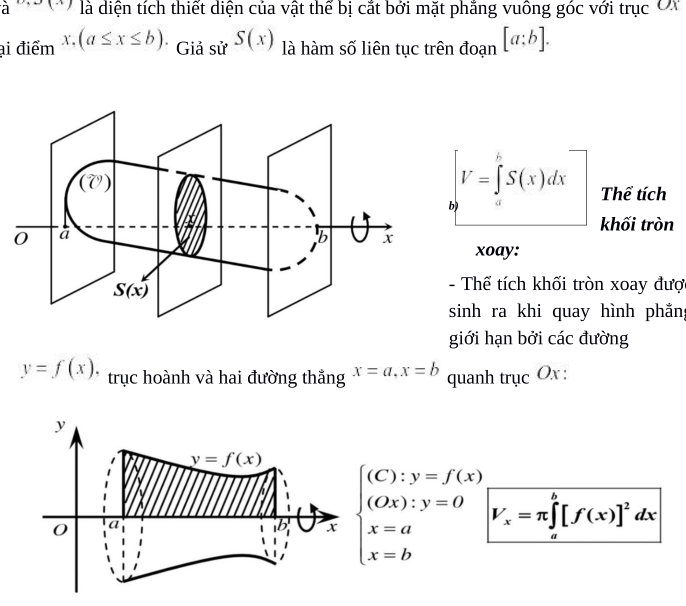
- Tích phân xác định: Đây là dạng bài tập yêu cầu tính giá trị của tích phân trên một khoảng xác định. Ví dụ, tính tích phân xác định của hàm số f(x) = x^2 từ x = 0 đến x = 2 có thể xuất hiện trong bài thi thực hành.
- Tích phân từng phần: Khi đối mặt với các tích phân phức tạp, kỹ thuật tích phân từng phần trở thành một công cụ hữu ích. Dạng bài tập này thường yêu cầu các kỹ thuật thay đổi biểu thức sao cho dễ tính toán hơn.
- Tích phân đổi biến: Đây là một trong những kỹ thuật phổ biến nhất để đơn giản hóa quá trình tính toán. Điều này giúp cho việc xử lý các hàm phức tạp trở nên dễ dàng hơn.

Phương Pháp Giải Cụ Thể và Hiệu Quả
Để giải quyết các bài tập tích phân trong kỳ thi CPII, bạn cần nắm vững cả lý thuyết lẫn thực hành. Dưới đây là một số phương pháp hiệu quả mà bạn có thể áp dụng:
- Hiểu rõ khái niệm tích phân: Việc nắm vững định nghĩa và ứng dụng của tích phân là bước đầu tiên và quan trọng nhất. Điều này không chỉ giúp bạn giải bài nhanh chóng mà còn giúp bạn hiểu sâu hơn về ý nghĩa của các kết quả đạt được.
- Ôn tập công thức tích phân cơ bản: Nắm rõ bảng nguyên hàm và các công thức tích phân cơ bản là điều không thể thiếu trước khi bước vào giải bài. Bạn cũng nên dành thời gian để làm quen với các dạng bài tập khác nhau để nâng cao khả năng phản xạ trong kỳ thi.
- Phân tích bài toán: Trước khi bắt đầu tính toán, hãy đọc kỹ đề bài và xác định rõ loại tích phân cần giải. Việc này giúp bạn tránh được những sai sót không đáng có và tiết kiệm thời gian.
Một Số Bài Tập Minh Họa
Việc thực hành là một phần không thể thiếu trong việc chuẩn bị cho kỳ thi. Dưới đây là một vài bài tập minh họa để bạn có thể tham khảo và luyện tập:
- Bài tập 1: Tính tích phân xác định của hàm số f(x) = 2x + 3 từ x = 1 đến x = 4.
Giải: Tích phân xác định của f(x) từ 1 đến 4 là: [ \int_{1}{4} (2x + 3) dx = [x^2 + 3x]_{1}{4} = (4^2 + 34) – (1^2 + 31) = 28 – 4 = 24. ]
- Bài tập 2: Tính tích phân từng phần của hàm số f(x) = x e^x.
Giải: Sử dụng công thức tích phân từng phần: [ \int u dv = uv – \int v du ] Đặt ( u = x ), ( dv = e^x dx ). Khi đó, ( du = dx ), ( v = e^x ).
[ \int x e^x dx = x e^x – \int e^x dx = x e^x – e^x + C. ]
- Bài tập 3: Giải phương trình vi phân dy/dx + y = e^(-x) với điều kiện ban đầu y(0) = 1.
Giải: Đây là phương trình vi phân tuyến tính bậc nhất. Bước 1: Tìm hệ số tích phân (integrating factor): [ μ(x) = e^{(\int 1 dx)} = e^x. ] Bước 2: Nhân cả hai vế của phương trình với μ(x): [ e^x dy/dx + e^x y = 1. ] Bước 3: Viết lại vế trái dưới dạng đạo hàm của tích: [ d/dx (e^x y) = 1. ] Bước 4: Tích phân cả hai vế: [ \int d/dx (e^x y) dx = \int 1 dx \Rightarrow e^x y = x + C. ] Bước 5: Sử dụng điều kiện ban đầu y(0) = 1: [ e^0 * 1 = 0 + C \Rightarrow C = 1. ] Bước 6: Giải cho y: [ y = (x + 1)e^{-x}. ]
Kết luận
Tích phân là một phần quan trọng trong kỳ thi CPII, và việc nắm vững kiến thức về tích phân sẽ giúp bạn giải quyết hiệu quả các bài toán liên quan đến tự động hóa và điều khiển công nghiệp. Bằng việc hiểu rõ vai trò của tích phân, nắm vững các loại bài tập thường gặp, áp dụng các phương pháp giải hiệu quả, và lưu ý những vấn đề cần thiết, bạn hoàn toàn có thể tự tin chinh phục kỳ thi CPII và tiến xa hơn trên con đường sự nghiệp trong lĩnh vực công nghiệp tự động hóa.

