CPII Việt Nam

Trong lĩnh vực toán học, đặc biệt là hình học, tam giác vuông đóng một vai trò vô cùng quan trọng. Hiểu rõ về các trường hợp đồng dạng của tam giác vuông không chỉ giúp học sinh nắm vững kiến thức cơ bản mà còn mở ra cánh cửa để tiếp cận những ứng dụng phức tạp hơn trong thực tế. CPII Việt Nam, với sứ mệnh nâng cao chất lượng giáo dục, xin giới thiệu bài phân tích chi tiết về chủ đề này.

1. Giới thiệu về tam giác vuông và tính đồng dạng

1.1 Định nghĩa tam giác vuông

Tam giác vuông là tam giác có một góc vuông (90 độ). Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền, hai cạnh còn lại được gọi là các cạnh góc vuông.

1.2 Khái niệm về tính đồng dạng

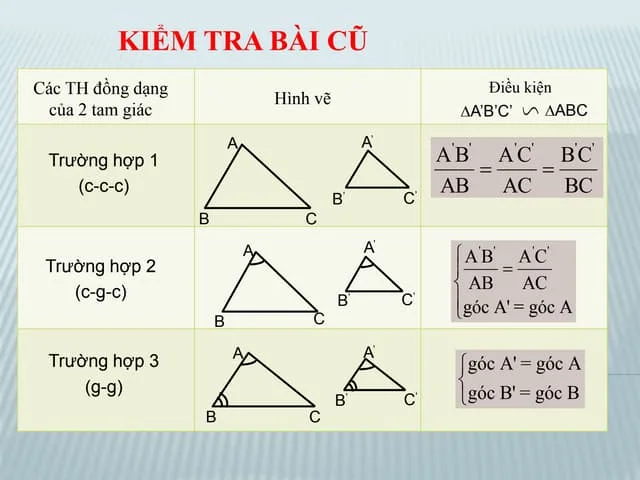
Hai hình được gọi là đồng dạng nếu chúng có cùng hình dạng nhưng kích thước có thể khác nhau. Đối với các tam giác, tính đồng dạng được xác định bởi sự tương đồng về các góc và tỷ lệ giữa các cạnh tương ứng.

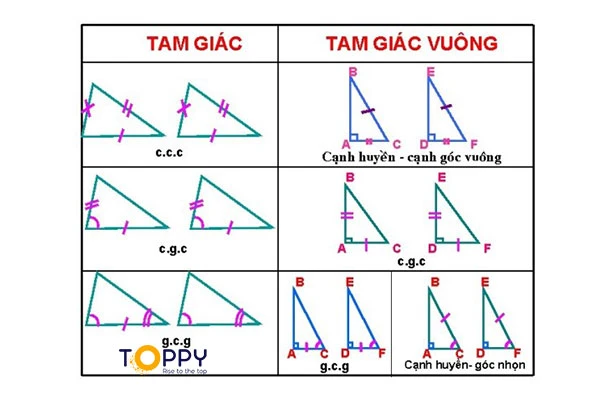
2. Các trường hợp đồng dạng của tam giác vuông

Có ba trường hợp chính để xác định sự đồng dạng giữa các tam giác vuông. Mỗi trường hợp đều có những đặc điểm riêng và cách áp dụng cụ thể.

2.1 Trường hợp 1: Góc – Góc (GG)

Hai tam giác vuông đồng dạng nếu chúng có một góc nhọn bằng nhau (ngoài góc vuông chung).

Lý giải:

• Tổng các góc trong một tam giác là 180°.
• Nếu hai tam giác vuông có một góc nhọn bằng nhau, góc nhọn còn lại cũng sẽ bằng nhau (vì 180° – 90° – góc nhọn đã biết).
• Do đó, hai tam giác có ba góc bằng nhau, chứng tỏ chúng đồng dạng.

Ví dụ:

Xét hai tam giác vuông ABC và DEF, với ∠B = ∠E = 90° và ∠A = ∠D. Ta có thể kết luận ABC đồng dạng với DEF.

2.2 Trường hợp 2: Cạnh huyền – Cạnh góc vuông (HC)

Hai tam giác vuông đồng dạng nếu tỷ lệ giữa cạnh huyền và một cạnh góc vuông của tam giác này bằng tỷ lệ tương ứng ở tam giác kia.

Lý giải:

• Nếu tỷ lệ này bằng nhau, nó xác định một góc nhọn giống nhau trong cả hai tam giác.
• Kết hợp với góc vuông sẵn có, ta có đủ điều kiện để kết luận hai tam giác đồng dạng (theo trường hợp GG).

Ví dụ:

Xét hai tam giác vuông ABC và DEF, với ∠B = ∠E = 90°. Nếu AB/BC = DE/EF, ta có thể kết luận ABC đồng dạng với DEF.

2.3 Trường hợp 3: Cạnh góc vuông – Cạnh góc vuông (CC)

Hai tam giác vuông đồng dạng nếu tỷ lệ giữa hai cạnh góc vuông của tam giác này bằng tỷ lệ tương ứng ở tam giác kia.

Lý giải:

• Tỷ lệ giữa hai cạnh góc vuông xác định tangent của một góc nhọn.
• Nếu tỷ lệ này bằng nhau ở hai tam giác, chứng tỏ chúng có một góc nhọn bằng nhau.
• Kết hợp với góc vuông sẵn có, ta có đủ điều kiện để kết luận hai tam giác đồng dạng (theo trường hợp GG).

Ví dụ:

Xét hai tam giác vuông ABC và DEF, với ∠B = ∠E = 90°. Nếu BC/AB = EF/DE, ta có thể kết luận ABC đồng dạng với DEF.

3. Ứng dụng của các trường hợp đồng dạng tam giác vuông

Hiểu rõ về các trường hợp đồng dạng của tam giác vuông mở ra nhiều ứng dụng quan trọng trong thực tế và trong các bài toán hình học phức tạp hơn.

3.1 Trong xây dựng và kiến trúc

Các nguyên tắc về đồng dạng tam giác vuông được áp dụng rộng rãi trong việc tính toán chiều cao của các công trình cao tầng, thiết kế cầu thang, và nhiều ứng dụng khác trong lĩnh vực xây dựng.

3.2 Trong đo đạc địa hình

Kỹ thuật đo đạc sử dụng nhiều nguyên lý của đồng dạng tam giác vuông để xác định khoảng cách và độ cao của các điểm không thể tiếp cận trực tiếp.

3.3 Trong thiết kế công nghiệp

Việc thiết kế các bộ phận máy móc, đặc biệt là các chi tiết có góc nghiêng, thường áp dụng các nguyên tắc của đồng dạng tam giác vuông.

4. Phương pháp giải các bài toán liên quan đến đồng dạng tam giác vuông

Để giải quyết hiệu quả các bài toán về đồng dạng tam giác vuông, học sinh cần nắm vững một số phương pháp cơ bản:

4.1 Phương pháp xác định trường hợp đồng dạng

• Xác định rõ các yếu tố đã biết trong đề bài.
• Kiểm tra xem các yếu tố này thỏa mãn điều kiện nào trong ba trường hợp đồng dạng.

4.2 Phương pháp thiết lập tỷ lệ

• Sau khi xác định được sự đồng dạng, thiết lập các tỷ lệ giữa các cạnh tương ứng.
• Sử dụng các tỷ lệ này để tìm ra các giá trị chưa biết.

4.3 Phương pháp kết hợp với các định lý khác

• Kết hợp kiến thức về đồng dạng tam giác vuông với các định lý khác như định lý Pythagoras, định lý sin, định lý cosin để giải quyết các bài toán phức tạp hơn.

5. Một số bài toán minh họa

Để giúp học sinh hiểu rõ hơn về cách áp dụng các trường hợp đồng dạng tam giác vuông, chúng ta sẽ xem xét một số bài toán cụ thể:

Bài toán 1:

Cho tam giác vuông ABC có góc vuông tại B. Từ B kẻ đường cao BD. Chứng minh rằng các tam giác ADB và BDC đồng dạng với tam giác ABC.

Lời giải:

• Tam giác ADB đồng dạng với ABC vì:
• Chúng có góc vuông chung tại B
• ∠BAD = ∠A (góc đỉnh)
  Theo trường hợp GG, ADB đồng dạng với ABC.
• Tương tự, tam giác BDC đồng dạng với ABC vì:
• Chúng có góc vuông chung tại B
• ∠BCD = ∠C (góc đỉnh)
  Theo trường hợp GG, BDC đồng dạng với ABC.

Bài toán 2:

Trong tam giác vuông ABC, góc A = 30°, BC = 10cm. Tính độ dài các cạnh còn lại của tam giác.

Lời giải:

• Trong tam giác vuông 30°-60°-90°, tỷ lệ các cạnh là 1 : √3 : 2
• BC là cạnh huyền, nên BC = 2x, với x là độ dài cạnh ngắn nhất
• Ta có: 2x = 10 → x = 5
• Do đó: AB (cạnh đối diện góc 30°) = 5cm
• AC (cạnh đối diện góc 60°) = 5√3 ≈ 8.66cm

6. Lưu ý khi học và áp dụng các trường hợp đồng dạng tam giác vuông

Để nắm vững và áp dụng hiệu quả kiến thức về đồng dạng tam giác vuông, học sinh cần lưu ý một số điểm sau:

6.1 Hiểu rõ định nghĩa và điều kiện

Nắm chắc định nghĩa của tam giác vuông và các điều kiện cần và đủ cho sự đồng dạng.

6.2 Thực hành đều đặn

Giải nhiều bài tập đa dạng để làm quen với các tình huống khác nhau và nâng cao kỹ năng áp dụng lý thuyết.

6.3 Kết hợp với các kiến thức khác

Liên kết kiến thức về đồng dạng tam giác vuông với các phần khác của hình học như tỷ số lượng giác, định lý Pythagoras để có cái nhìn toàn diện hơn.

6.4 Ứng dụng vào thực tế

Tìm hiểu và khám phá các ứng dụng thực tế của đồng dạng tam giác vuông để tăng hứng thú học tập.

7. Tài nguyên học tập bổ sung từ CPII Việt Nam

CPII Việt Nam cam kết cung cấp các tài nguyên học tập chất lượng cao để hỗ trợ học sinh trong việc nắm vững kiến thức về đồng dạng tam giác vuông và các chủ đề toán học khác.

7.1 Khóa học trực tuyến

Truy cập cpiivietnam.org để tìm hiểu về các khóa học trực tuyến chuyên sâu về hình học, bao gồm cả chủ đề đồng dạng tam giác vuông.

7.2 Tài liệu tham khảo

CPII Việt Nam cung cấp các tài liệu tham khảo chất lượng cao, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm. Các tài liệu này có thể được tải về từ website của chúng tôi.

7.3 Hỗ trợ trực tuyến

Học sinh có thể nhận được sự hỗ trợ trực tiếp từ đội ngũ giáo viên của CPII Việt Nam thông qua các kênh sau:

• Hotline: 0909 102 102
• Email: [email protected]

7.4 Workshops và seminar

CPII Việt Nam thường xuyên tổ chức các buổi workshop và seminar về các chủ đề toán học, bao gồm cả đồng dạng tam giác vuông. Thông tin về các sự kiện này được cập nhật thường xuyên trên website của chúng tôi.

Kết luận

Hiểu rõ về các trường hợp đồng dạng của tam giác vuông là một bước quan trọng trong việc nắm vững kiến thức hình học. Kiến thức này không chỉ giúp học sinh giải quyết hiệu quả các bài toán trong chương trình học mà còn mở ra cánh cửa để tiếp cận những ứng dụng thực tế phong phú.

CPII Việt Nam, với sứ mệnh nâng cao chất lượng giáo dục, luôn sẵn sàng hỗ trợ học sinh trong hành trình khám phá toán học. Chúng tôi tin rằng với sự hỗ trợ đúng đắn, mỗi học sinh đều có thể phát triển tư duy logic và kỹ năng giải quyết vấn đề thông qua việc học tập toán học.