CPII Việt Nam

I. Định nghĩa

Hai đường thẳng được gọi là chéo nhau khi chúng không song song và không cắt nhau trong không gian ba chiều. Điều này chỉ có thể xảy ra trong không gian ba chiều, không thể xảy ra trong mặt phẳng.

II. Đặc điểm cơ bản

1. Khoảng cách giữa hai đường thẳng chéo nhau

• Luôn tồn tại và duy nhất
• Là đoạn thẳng ngắn nhất nối hai đường thẳng
• Vuông góc với cả hai đường thẳng

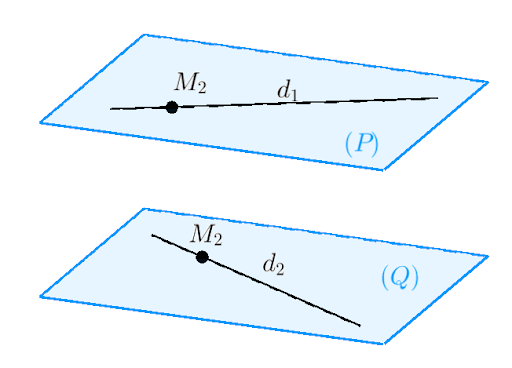
1. Mặt phẳng song song chứa hai đường thẳng

• Hai đường thẳng chéo nhau luôn xác định hai mặt phẳng song song
• Mỗi mặt phẳng chứa một trong hai đường thẳng

III. Phương pháp xác định hai đường thẳng chéo nhau

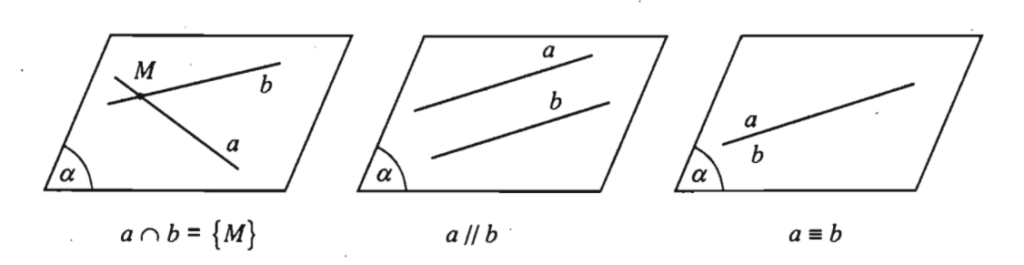
1. Phương pháp véc-tơ chỉ phương

• Nếu hai đường thẳng có véc-tơ chỉ phương không song song
• Và không có điểm chung
• Thì hai đường thẳng đó chéo nhau

1. Phương pháp tọa độ
   Cho hai đường thẳng:

   d1: (x = x1 + a1t
        y = y1 + b1t    (t ∈ R)
        z = z1 + c1t)

   d2: (x = x2 + a2s
        y = y2 + b2s    (s ∈ R)
        z = z2 + c2s)

Hai đường thẳng chéo nhau khi và chỉ khi:

• Véc-tơ chỉ phương không song song: (a1,b1,c1) không cùng phương với (a2,b2,c2)
• Hệ phương trình xác định điểm chung vô nghiệm

IV. Các tính chất quan trọng

1. Góc giữa hai đường thẳng chéo nhau

• Được xác định bởi góc giữa các véc-tơ chỉ phương
• Công thức: cos φ = |a1a2 + b1b2 + c1c2|/√[(a1² + b1² + c1²)(a2² + b2² + c2²)]

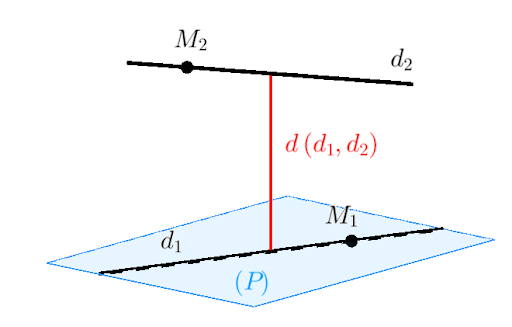
1. Khoảng cách giữa hai đường thẳng chéo nhau

• Công thức: d = |[(M1M2,v̅1,v̅2)]|/|[v̅1,v̅2]|
  Trong đó:
• M1M2 là véc-tơ nối hai điểm bất kỳ trên hai đường thẳng
• v̅1, v̅2 là véc-tơ chỉ phương của hai đường thẳng
• [a,b,c] là tích hỗn tạp của ba véc-tơ

V. Ví dụ và bài tập

Ví dụ 1:

Xét hai đường thẳng:

d1: (x = 1 + 2t
     y = 2 + t     (t ∈ R)
     z = 1 + t)

d2: (x = 2 + s
     y = 1 + 2s    (s ∈ R)
     z = 3 - s)

Chứng minh rằng hai đường thẳng này chéo nhau.

Lời giải:

1. Kiểm tra véc-tơ chỉ phương:

• v̅1 = (2,1,1)
• v̅2 = (1,2,-1)
  → Không song song (không tỉ lệ)

1. Giải hệ phương trình để tìm điểm chung:

   1 + 2t = 2 + s
   2 + t = 1 + 2s
   1 + t = 3 - s

Hệ vô nghiệm → Không có điểm chung

Vậy hai đường thẳng chéo nhau.

Bài tập tự luyện:

1. Cho hai đường thẳng:

   d1: (x = 1 + t
        y = 2 - t     (t ∈ R)
        z = t)

   d2: (x = 3 + 2s
        y = 1 + s     (s ∈ R)
        z = 2 - s)

Hãy:
a) Chứng minh hai đường thẳng chéo nhau
b) Tính khoảng cách giữa hai đường thẳng
c) Tính góc giữa hai đường thẳng

2. Cho hai đường thẳng:

   d1: A1(1,2,3) và véc-tơ chỉ phương v̅1(1,1,1)
   d2: A2(0,1,2) và véc-tơ chỉ phương v̅2(1,-1,1)

Chứng minh hai đường thẳng chéo nhau và tính khoảng cách giữa chúng.

VI. Ứng dụng trong thực tế

1. Trong kiến trúc

• Thiết kế cấu trúc không gian
• Tính toán khoảng cách an toàn giữa các thanh dầm

1. Trong robot học

• Tính toán chuyển động của cánh tay robot
• Tránh va chạm giữa các bộ phận

VII. Lưu ý khi giải bài tập

1. Các bước cơ bản

• Xác định véc-tơ chỉ phương
• Kiểm tra tính song song
• Kiểm tra sự tồn tại điểm chung

1. Lỗi thường gặp

• Nhầm lẫn với đường thẳng cắt nhau
• Quên kiểm tra điều kiện không có điểm chung
• Sai sót trong tính toán véc-tơ chỉ phương

Để tìm hiểu thêm về chủ đề này và nhiều bài tập khác, vui lòng truy cập: cpiivietnam.org

Thông tin liên hệ:
Hotline: 0909 102 102
Email: [email protected]
Website: cpiivietnam.org
Địa chỉ: 105 Tôn Dật Tiên, Phường Tân Phú, Quận 7, Thành phố Hồ Chí Minh